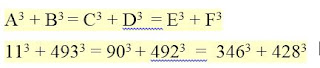Friedman Number

A Friedman number is a positive integer which can be written with the help of symbols like - + , - , x, / , (), ^ etc. and using the digits of the numbers.

Example:-
25, 121, 125, 126, 127, 128, 153, 216, 289, 343, 347, 625, 688, 736, 1022, 1024,
1206, 1255, 1260, 1285, 1296, 1395, 1435, 1503, 1530, 1792, 1827, 2048, 2187, 2349,
2500, 2501, 2502, 2503, 2504, 2505, 2506, 2507, 2508, 2509, 2592 ,2737, 2916, 3125,
3159, 3281, 3375, 3378, 3685, 3784, 3864, 3972, 4088, 4096, 4106, 4167, 4536, 4624,
4628, 5120, 5776, 5832, 6144, 6145, 6455, 6880, 7928, 8092, 8192, 9025, 9216, 9261.

Explanation:-
25 = 5^2
121 = 11^2
125 = (5)^1 + 2 = 5 ^3
126 = 21 x 6
127 = -1 + 2^7
289 = (8 + 9)^2
343 = (3 + 4 ) ^3

Friedman numbers are named after Erich Friedman, an Associate Professor of Mathematics in Florida in US.


Enjoy
Rajesh Thakur

References:-
1. https://en.wikipedia.org/wiki/Friedman_number
2. http://www2.stetson.edu/~efriedma/mathmagic/0800.html

RAMANUJAN TRIPLES

A number that can be written as the sum of cubes of a number in three ways.

This is also known as TAXICAB 3

DR RAJESH KUMAR THAKUR

Ramanujan Number

Ramanujan was fond of numbers. Prof Hardy once visited the hospital to see the ailing Ramanujan riding on a taxi. The taxi number was 1729. This 1729 is called the Ramanujan Number.

C P Show in his book wrote -
“Hardy used to visit him, as he lay dying in hospital at Putney. It was on one of those visits that there happened the incident of the taxicab number. Hardy had gone out to Putney by taxi, as usual his chosen method of conveyance. He went into the room where Ramanujan was lying. Hardy, always inept about introducing a conversation, said, probably without a greeting, and certainly as his first remark: ‘I thought the number of my taxicab was 1729. It seemed to me rather a dull number.’ To which Ramanujan replied: ‘No, Hardy! No, Hardy! It is a very interesting number. It is the smallest number expressible as the sum of two cubes in two different ways.’”

a^ 3 + b^ 3 = x where x is the Ramanujan Number

This number is also known as TAXI CAB number.

Thanks for reading

Dr Rajesh Kumar Thakur

Kaprekar number

Kaprekar Number

                                                             D R Kaprekar (1905 - 1986)

A Kaprekar number is a special n digit number such that if it is squared the sum of the squared quantity’s right most n digits and remaining part are equal to the number itself.

45^2 = 2025 and 20 + 25 = 45

703^2 = 494 209 and 494 + 209 = 703

99^2 = 9801 and 98 + 01 = 99

The first few Kaprekar numbers are -
1, 9, 45, 55, 99, 297, 703, 999, 2223, 2728, 4879, 4950, 5050, 5292, 7272, 7777, 9999, 17344, 22222, 38962, 77778, 82656, 95121, 99999, 142857, 148149, 181819, 187110, 208495, 318682, 329967, 351352, 356643,-----

The Kaprekar numbers were named after Shri Dattathreya Ramchandra Kaprekar who discovered them.


Dr Rajesh Kumar Thakur

Truncating Primes

Truncating Primes

There are few primes which remain Primes after chopping off their last digits.
73939133
7393913
739391
73939
7393
739
73
7

Let’s enjoy another
31
331
3331
33331
333331
3333331
33333331
Besides that 58393339, 37337999 …. are truncated Primes.


Dr Rajesh Kumar Thakur

Palindrome Number

Palindromic Number:- Numbers which remains the same when read from the left to right or vice-versa. Indian mathematician Mahavira has mentioned about this in his book.
e.g. 15151, 11000011000011.

If you want to make any number Palindromic here is the simple way :-
Take a number 19
Reverse its digits + 91

Sum it 110
Reverse the digit + 011

Sum it 121

The process will be repeated until you get a palindromic number.

There are several Palindromes number. Mahavira called it पुष्प माल संख्या (garland number).

(Read about Palindrome Primes at -http://www.magic-squares.net/primes.htm)

There are several magic squares formed with the help of Palindromes number.

(Acknowledgement :- I acknowledge the effort by the above mentioned websites for their contribution in the field of Mathematics.I have tried to put their websites for further reference)

Dr Rajesh Kumar Thakru

Friend Or Amicable Numbers

                                         Amicable /Friend Numbers

Two numbers are called Amicable if each of which is equal to the sum of all the exact divisors of the other except the number itself. 220 and 284 are the first pair of amicable numbers.

220 has the exact divisors 1,2,4,5,10,11,20,22,44,55 and 110 whose sum is 284 

1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284

and 284 has the exact divisors 1, 2, 4, 71, and 142 whose sum is 220. 

1 + 2 + 4 + 71 + 142 = 220

Another pair of amicable number is 1184 and 1210.

The set of 220 and 284 was the first known set of amicable numbers. Pythagoras discovered the relationship and coined the term Amicable because he considered the numbers to be a symbol of friendship.

There is an unauthenticated story related to Amicable numbers that a prince whose name from the stand point of numerology was equivalent to 284 sought a bride whose name would represent 220 believing the fact that such combination would guarantee for a happy marriage throughout the life.

Here is the list of first ten Amicable Pairs:-


1 ---  (220 ,284)
2 --- (1184 , 1210)
3 --- (2620 , 2924)
4 ---  (5020 ,5564 )
5 ---  (6232 ,6368)
6 ---  (10744 ,10856)
7 -- (12285, 14595)
8 -- (17296 , 18416)
9 -- (63020 , 76048)
10 -- (66928 , 66992)

An Arab Mathematician tried to generalize a rule to find the Amicable Number but he could not succed completely. The Thābit ibn Qurra theorem is a method for discovering amicable numbers invented in the ninth century by the Arab mathematician Thābit ibn Qurra.

It states that if

where n > 1 is an integer and p, q, and r are prime numbers, then 2^n×p×q and 2^n ×r are a pair of amicable numbers.

Dr Rajesh Kumar Thakur